webdesignlooki.blogg.se - Tangent line equation calculator

Tangent line equation calculator how to#
Tangent line equation calculator trial#
Tangent line equation calculator free#

The average satisfaction rating for the company is 4.7 out of 5.

Tangent line equation calculator free#

Therefore, the equation of the tangent line is 12x - y - 12 = 0įind the equation of the tangent line for the given function f(x) = xln(x) at x = 1 and verify it using the online tangent line calculator. Free tangent line calculator - find the equation of the tangent line given a point or the intercept step-by-step Average satisfaction rating 4.7/5. Substituting the value of x in the above equation, we getĮquation of tangent line having slope f'(x) = 12 and passing through (2, 12) is

Tangent line equation calculator trial#

With Cuemath, find solutions in simple and easy steps.īook a Free Trial Class Solved Examples on Tangent Line Calculatorįind the equation of the tangent line for the given function f(x) = 3x 2 at x = 2 and verify it using the online tangent line calculator. Use our free online calculator to solve challenging questions. Substitute the values in this equation to find the tangent line equation. Thus, using this concept, the equation of a tangent can be given as y - y 1 = f'(x) (x - x 1).According to the point-slope form, the equation of a line passing through some point (x 0, y 0) with a slope m is given as y - y 0 = m (x - x 0).This will give us the slope of the tangent. Substitute the value of the x coordinate in f'(x).Differentiate the given function of the curve f'(x).We can calculate the slope of the secant line using.

Tangent line equation calculator how to#

This gives us the y coordinate, y 1, of the point of intersection. How To Find Secant Line EquationSecant Lines and Tangent Lines. Substitute the value of the x coordinate, x 1, in the given function f(x).Then we can follow the steps given below to find the equation of the tangent. Suppose we know the function of the curve, f(x), that the tangent touches and the x coordinate, x 1, of the point of intersection. In this section we want to find the tangent lines to the parametric equations given by, x f (t) y g(t) x f ( t) y g ( t) To do this let’s first recall how to find the tangent line to y F (x) y F ( x) at x a x a. If we take the first-order derivative of the given function and evaluate it at the point of intersection, we can find the slope of a tangent. Section 9.2 : Tangents with Parametric Equations.

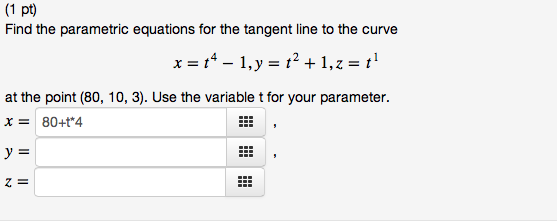
To determine the equation of a tangent, we need to know the slope of the line as well as the point where it touches the curve.

Step 4: Click on the " Reset" button to clear the fields and enter new values.

Step 3: Click on the " Calculate" button to find the equation of the tangent line.

Step 2: Enter the values in the given input boxes.

Step 1: Go to online tangent line calculator.

Please follow the steps given below to find the equation of the tangent line using the online tangent line calculator: To use the tangent line calculator, enter the values in the given input boxes. The point-slope form of a line can be used to find the equation of a tangent. Tangent Line Calculator is an online tool that helps to find the equation of the tangent line to a given curve when we know the x coordinate of the point of intersection. A tangent is a line or a plane that touches a curve or a curved surface at exactly one point. In geometry, a tangent is the line drawn from an external point and passes through a point on the curve. Lastly, we will write the equation of the tangent line and normal lines using the point (1,8) and slope tangent slope of m = 16.64 and normal slope of -0.06, respectively.Tangent Line Calculator is used to determine the equation of a tangent to a given curve. This means that the slope of the tangent line is 16.64, and the slope of the normal line is -1/16.64 or -0.06, which is the negative reciprocal slope! All we will do is substitute the given information into the point-slope formula and simplify, as indicated below. So, what do we remember about equations for lines?įor instance, if we desired to write the equation of a line given the point (6,1) and slope m = 3. Jenn, Founder Calcworkshop ®, 15+ Years Experience (Licensed & Certified Teacher)īecause if we are ever asked to solve problems involving the slope of a tangent line, all we need are the same skills we learned back in algebra for writing equations of lines. Tangent line calculator f(x) x0 Calculate The tool that we put at your disposal here allows you to find the equation of the tangent line to a curve in a.